標準偏差とは何か！その求め方と意味を図解で徹底解説

ここでは高校数学で登場し、統計学を学ぶ上でとても重要な役割を担う「標準偏差」について、図解を駆使し、その求め方と意味について解説していきます。

標準偏差の求め方や意味を理解するには、以下の4つのSTEPを踏めば簡単に理解することができます。

標準偏差は「式を覚える」のではなく「イメージ化」することがとても重要です。

4つのSTEPを本質的なイメージで捉えることで「標準偏差とは何か」や「標準偏差はどうやって求めるのか」がスッキリ頭に入ってきますので、ぜひ最後までお付き合い下さい。

標準偏差の求め方

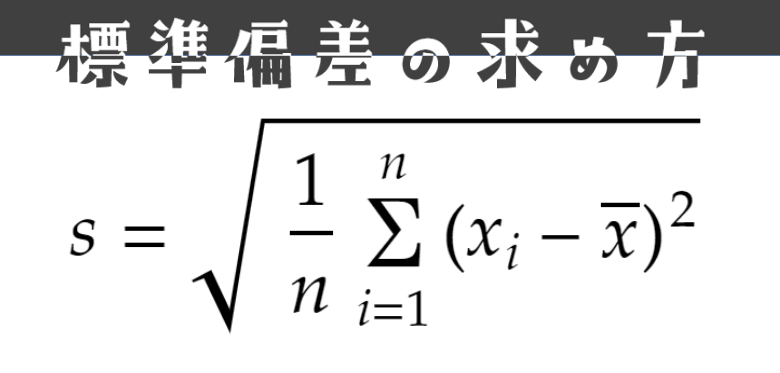
標準偏差を求める式がこちらになります。

いきなりかなり難しい式が登場してきました（汗

この式を覚えることはなかなか厳しいですよね。

ただ、この式の記号のひとつひとつをイメージ化しながら読み解くことで、この難しい式が実はとてもストーリー性のある面白い構造をしていることが分かってきます。

ここではそのひとつひとつのイメージ化と標準偏差を求めるためのストーリーを初めに述べた4つのSTEPに分け、図解しながら解説していきます。

平均値の求め方と意味

まず、１つめのSTEPとして「平均値」について説明します。

平均値は、テストの平均点や平均年収といった日常的に使われる指標ですので、すでにイメージを持てている方も多いと思いますが、念のため確認をしていきます。

平均値の求め方

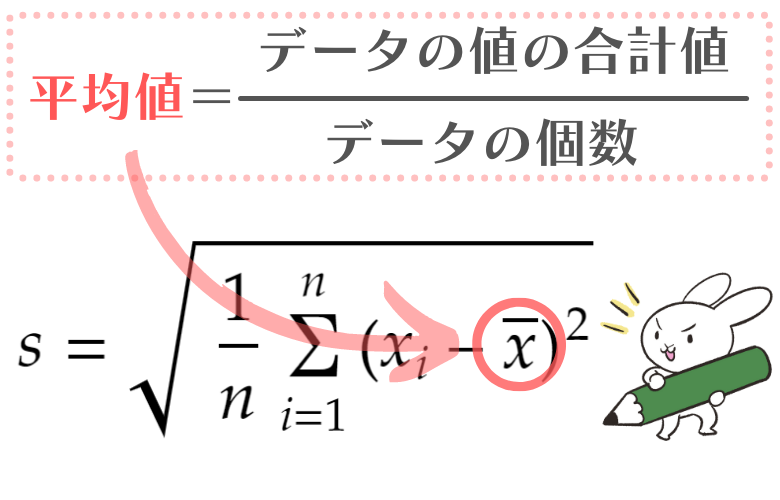
平均値の求め方は、テストの平均点の出し方と同じです。

平均値は、平均点や平均年収などを世の中の様々な場面で用いられているとても身近な指標ですが、その意味を見誤ると大きな失敗につながってしまうので要注意です。

平均値の意味

平均値の意味は、実は奥が深いのですが、ここではあくまで標準偏差への流れを理解するを目指した説明をします。

標準偏差を理解するためには、平均値は普通の人と理解しましょう。

基本的に、平均値という指標が有効に機能するためには、得られたデータの分布が正規分布であることが望ましいことが知られています。

正規分布とは、ざっくりいうと平均値にデータが集まり、左右対称に裾野が広がっている山のような状態の分布図を指します。

身長や体重、センター試験（現共通テスト）の点数などが正規分布となります。

つまり、平均値の付近に所属するデータが最も多く、それを私たちは日常的に「普通」と捉えています。

図でイメージするとこんな感じです。

以上より、平均値を求める意味としては普通の人がどのような状態にあるのかを求めていると理解しておきましょう。

偏差の求め方と意味

次にSTEP２の「偏差」という考え方をイメージ化していきます。

偏差は先ほどSTEP１で登場した平均値を用いて次のように計算します。

偏差の求め方

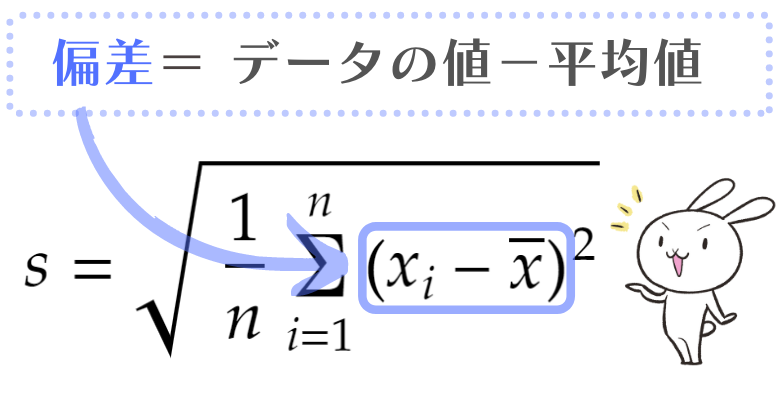
偏差はデータの値から平均値を引くことで得られる数値のことです。

平均点が60点のテストで、あなたの点数が80点だった場合、あなたの偏差は

となります。

一方、あなたの点数が40点だった場合の偏差は

となるため、偏差がマイナスになることも当然ありえます。

つまり、偏差とはどれほど「普通」から離れているのかを数値化していると頭に入れておけば、この偏差の式がしっかり頭に残ると思います。

偏差の意味

STEP１の平均値を「普通」とするならば、平均値から離れた値を取った人は、良い意味でも悪い意味でも「普通ではない人」と表現できます。

偏差という指標は、「普通ではない人＝変人」と考え、その人がどれほど変人であるのかを数値化した指標と覚えましょう。

つまり、偏差＝変さと言い換えます。

「偏差」という指標は、０より離れた人ほど変人であることを意味し、０に近い人ほど普通であることを意味する個人一人ひとりを評価する数値なのです。

偏差の平均をとる

では、この一人ひとりの偏差の平均値をとれば、一人ひとりではなくクラス全体の変人（普通）度合いが見えてくるのではないでしょうか。

例えば、平均点が同じ50点だったとしても、偏差という視点からクラス得点の分布図を見ると違う分析を行うことができます。

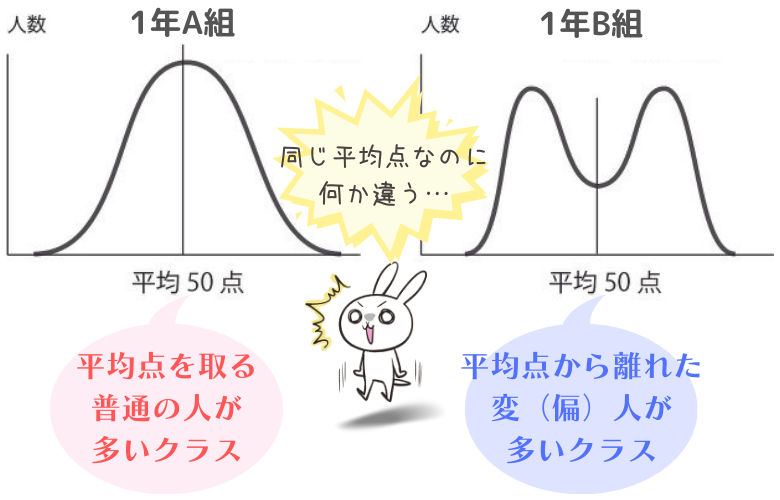
つまり、偏差の平均値をとれば平均点だけでは分からない「変人の多さ」という集団としての評価を数値化できると考えるわけです。

しかし、ここに大きな問題が潜んでいます。

その問題とは、平均値からどれほど離れているのかを数字で表した偏差ですが、偏差は偏差の平均を取ると常に０になってしまうのです。

偏差の平均が抱えるこの問題について、具体的な例を挙げて説明します。

今、10点満点の数学テストをある8人の集団で行ったところ、次のような結果が得られたとします。

この8名の平均点は、STEP１で学んだ平均値の式で計算します。

こうしてこのクラスの平均点が5点と分かったので、STEP２で学んだ偏差を算出します。

こうして得られた8人の偏差の平均値を計算すると

このように偏差の平均を取ると、どのようなデータ群であったとしても「０」となってしまうのです。

この理由を簡単に説明と、偏差にはプラスとマイナスの値がそれぞれ出現し、平均を取るとこれらがお互いに打ち消しあい、すべて加えると０になってしまうことで起こります。

平均値の意味を考えると、偏差の平均値が０になるのは当然といえるのですが、いずれにしても、どんなときも「0」になるなら使いものにはなりません。

偏差平方で問題解決

偏差を平均するとどんなデータでも０になってしまう問題を解決するために

1. 平均をとったとき０にはならず
2. データの特徴を把握できる

という指標に偏差を加工する必要があります。

それが「偏差平方」という考え方です。

偏差平方は、その名のとおり、偏差を平方（２乗）したものです。

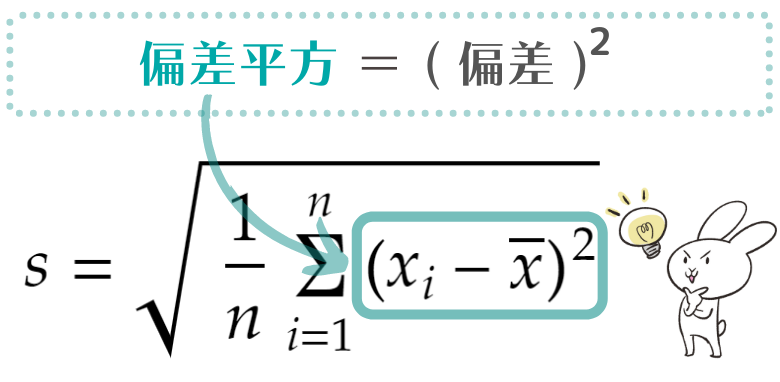
偏差を２乗することでマイナスの値はプラスの値に【（ー）×（－）＝（＋）】変わり、平均をとっても０になることはなくなります。このように偏差の問題点である平均を取ると０になるという特徴を克服した「偏差平方」という指標ができあがりました。

分散の求め方と意味

STEP２の最後に登場した偏差の平方（２乗）を平均した数値のことを「分散」と呼びます。

STEP３ではこの「分散」の求め方と意味について説明します。

分散の求め方

分散は、偏差平方を平均することで求まる値です。

偏差の平均は常に０になってしまいましたが、偏差平方はその問題点を克服した指標ですので平均することで値が求まります。

それが分散というわけです。

分散の意味

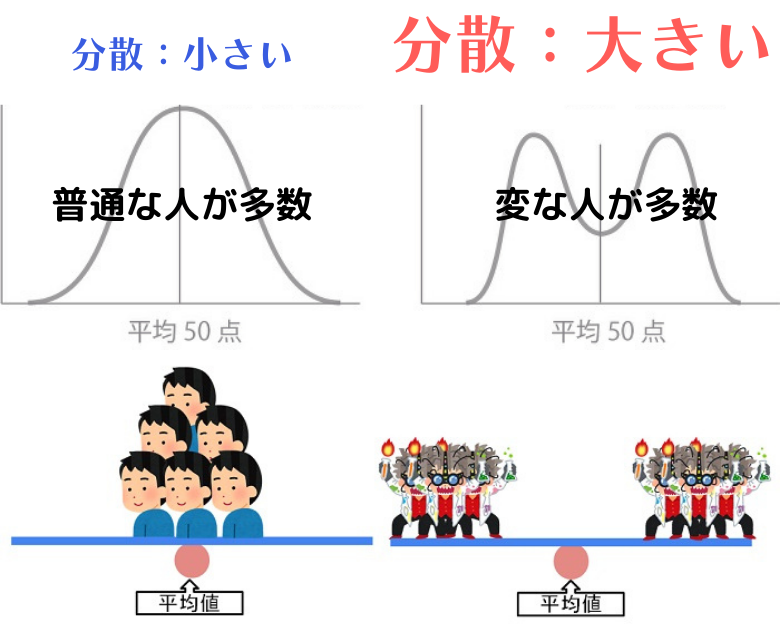
分散の意味は、その集団がどれだけ散らばった値（平均値から離れた値）を取ったのかを数値化した散らばり具合を表している指標です。

分散が小さいということは普通の人が多い集団であるのに対し、分散が大きいということは平均から離れた変人が多い集団であることを意味します。

具体例で考えてみよう

では、実際に具体的な事例をもとにSTEP１「平均値」からSTEP３「分散」までの一連の流れを具体例を用いて計算してみましょう。

上でも取り上げた10点満点の数学テストをある8人の集団で行ったデータで分散を計算していきます。

各データの偏差を求めるところまでは上で説明しましたので、ここからは偏差平方から分散を求めていきます。

上の表の偏差を2乗した偏差平方（一番右）の平均を取れば分散が求まります。

このデータ群の平均値からの散らばり度合いは「４」と分散を計算することで数値化できたことになります。

分散の問題点

一見すると、分散には何の問題もないように思えるのですが、実はこの分散という指標には大きな欠点が潜んでいます。

分散の欠点は何かというと、次の２つのことが大きな問題となります。

どちらの問題も分散を求める過程で行った偏差平方が原因といえます。

では、一つ一つ説明します。

値が大きくなりすぎる

データを平方（2乗）するということは、扱うデータによっては非常に大きな数値を扱う必要が出てきてしまうのです。

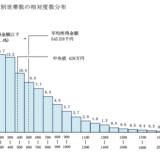
上で紹介した数学の点数くらいなら大した問題になりませんが、扱う数値が年収だったとしたらどうでしょう。

年収１億円の人の偏差平方を計算すると「兆」という単位を超えるほど、むちゃくちゃ大きな数字になってしまいます。

いくら計算処理技能が向上したPCなどがあるといえども、あまりに大きな数字を使うことは決していいことではありません。これが分散の１つ目の欠点です。

単位が変わってしまう

２つ目の分散の欠点は、偏差を平方したことで単位が変わってしまうという点です。

例えば「㎝」を２乗した値は「㎠」です。

扱っている次元が変化してしまうわけですからこれは大変大きな問題です。

そこで、最後のステップとして「標準偏差」という指標が必要になってくるというわけです。

標準偏差の求め方と意味

分散の２つの欠点を、一瞬で解決してくれる考え方が数学には存在します。

それがルート（√）です。

分散で求めた値のルートを取ることで、分散の欠点である

という問題をどちらも解決してくれます。

標準偏差の求め方

分散の平方根を取ることで、分散の特性を残しつつも、大きくなりすぎしまう欠点も単位が変化してしまう欠点も解消してくれます。 

こうしてようやく標準偏差にたどり着くことができました。

標準偏差の意味

標準偏差の意味は、分散と同じでデータの散らばりの度合いを示す値です。

標準偏差が大きいほど平均的な人が少なく、いろいろなタイプの人間がそこにいることを意味します。

逆に、標準偏差が０に近いほど平均的な人が集まった集団であることがわかります。

つまり、平均値だけでは分からないことが標準偏差から読み取れることになります。

標準偏差を知れば、行動が変わる

さて、本日学んだ「標準偏差」の求め方と意味は、理解できたでしょうか。

もう一度、標準偏差を求めるための４つのSTEPを簡単に振り返っておきます。

1. 平均値で”普通”を知る
2. 偏差で個人の”変さ”を知る
3. 分散で集団の”変さ”を知る
4. 分散は問題多いのでルートを取って標準偏差へ

本日は標準偏差とは何か、その意味と求め方について説明してきました。

この記事を読んで標準偏差が理解できた方は、次のステップとして２つのデータの関係を数値化する「相関係数」について学ぶことをおすすめします。

相関係数はここで学んだ標準偏差を使っていますので、標準偏差の学びがより深まります。

ぜひ、ここで一緒に勉強してきた平均値から標準偏差までの流れを理解し、実社会で意味を理解しながら使いこなせる標準偏差の達人を目指してください。