必要十分条件の意味と覚え方を図解で徹底解説！

ここでは、高校数学で学ぶ「必要十分条件」という考え方について、その意味と覚え方を分かりやすく解説していきます。

必要十分条件という考え方に対しては、苦手意識を持っている方も多いのではないでしょうか。ゴリゴリ計算する他の数学分野とは異なり、より論理的な思考力が求められる分野であるため、「よく分からない」とあきらめてしまいがちな概念です。

一方で、必要十分条件の考え方を理解し、使いこなすことができるようになると、高校生ならずとも社会人でも、他者に対し論理的に状況を説明・共有することができる大変便利な概念でもあります。

一見すると何を言っているのか分かりにくい分野ですが、その理解に必要な本質は驚くほど単純です。

そして、その本質を抑えてしまえば、入試問題はワンパターンに見えてきますし、日常生活でも実用性の高い考え方となっています。

そこで、ここでは、数学が苦手な方でも直感的に「必要十分条件」の本質に触れられる解説を目指していくことにします。

ということで、ここで解説する数学の知識は次の通りです。

数学が苦手な高校生や社会人の方にも、「なるほどな！」と思っていただけるよう図解や事例を取り入れていきますので、最後までお付き合いいただけたら嬉しいです。

他にも、統計学に関する記事を多く書いています。ぜひそちらも参考にしてみてください。

2021年10月12日標準偏差とは何か！その求め方と意味を図解で徹底解説

必要十分条件の考え方と意味

必要十分条件とは何かを語るためには、まず『命題』というものを知っておく必要があるので紹介します。

命題とは何か

言っていることは非常に簡単です。

イメージを持ってもらうために具体例を挙げますので、まずは命題とは何かを抑えていきましょう。

こうした文章は、命題ではない文章になります。

身長170㎝はバレーボール選手の中ではむしろ小柄でしょうし、年収600万円あっても借金がいくらかあれば裕福には暮らせません。妻に「うちの旦那は誰がどう見てもイケメンだよ！」なんて言ってほしいですが、顔の好みは人それぞれです。

このように感覚的な言葉や概念が入った文章は命題とは呼べません。

そして、命題と呼べない文章に対しては、必要十分条件という考え方は適応できないことになります。

それでは、命題である文章の例を挙げてみます。

命題とは何か分かっていただけたでしょうか。ちなみに、文章が正しいことを数学では『真』といい、間違っていることを『偽』といいます。

そして、真偽の判断ができる命題は、必ず次のような構造の文章となっています。

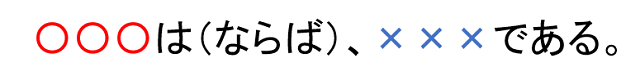
「○○○」と「×××」には固有名詞やグループ、数式などにより範囲が指定された条件がそれぞれ入ります。

ここまで理解できれば、本日のレポートテーマ「必要十分条件の意味」が見えてきます。

必要十分条件とは何か

２つの条件「○○○」と「×××」を以下での説明の便宜上それぞれを「P」と「Q」と文字で置くことにします。（記号を使って数学っぽくしただけ）

それでは、命題「Pは、Qである」を用いて、必要十分条件とは何かについて説明していくことにします。

まず、２つの条件「P」と「Q」は、以下の5つの構造いずれかに分類することができます。

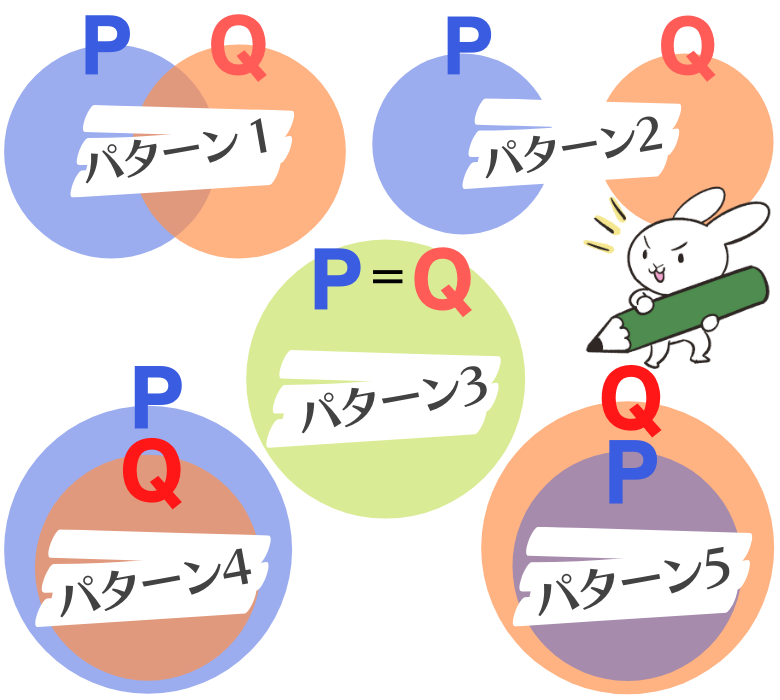
上の図は、条件「P」と「Q」を満たすものを袋に入れたように図で表しています。この図を数学ではベン図といいます。

そして、この５つの構造のうち、パターン３に該当する「P」と「Q」が対等である関係を「必要十分条件」と呼び、さらに、パターン４や５の構造を持つ条件に対し、どちらの条件がより厳しい条件かを相手に伝えていくために「必要条件」と「十分条件」という呼び名を使い分けていくことになります。

つまり、ここで示した構造を見抜くことこそ「必要十分条件」という分野の本質なのです。

なお、パターン１と２の構造は、必要条件や十分条件という考え方を用いるのに適していません。

なぜならば、この２つの構造は

• パターン１の例
  ➡ 晴れの日は、気温20℃を超える
• パターン２の例
  ➡ 猫は、犬である

というように、必ず偽と判定される命題になるからです。（パターン１の例は、冬は晴れても20℃以下になる日があるため、偽となります）

命題としては必ず偽となる構造なのですから、その構造に名前を付けるまでもないということです。

では、必要条件と十分条件について理解を深めていきましょう。

必要条件とは何か

必要条件とは、ある条件が成り立つために必要な条件になります。

例えば、

• 東京大学に合格するための必要条件は？

と言われたら、

1. 高校を卒業する（している）
2. 出願書類を提出する
3. 入試を受ける

などの条件を満たす必要があるわけです。

この例を用いて必要条件をベン図で表すと、どういった構造になっているかがよく分かります。

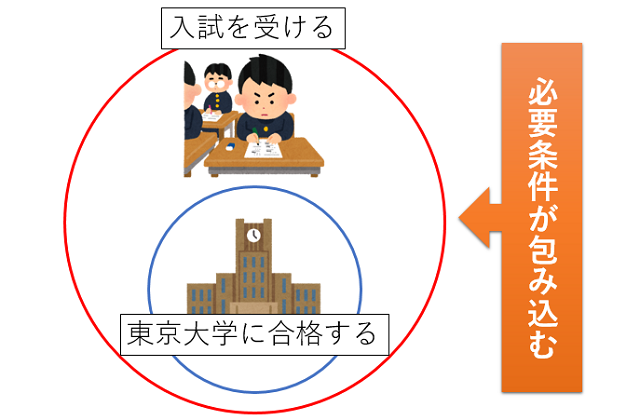
「東京大学に受かる」ための必要条件「入試を受ける」は、もとの条件をすっぽり覆っていることになります。

これは、東大に受かるためには入試を受ける必要があるが、入試を受けたから東大に受かるとは限らないということを意味しています。

このように提示された条件を包み込む条件のことを必要条件というわけです。

十分条件と何か 

一方の十分条件とは、 その条件を満たしていれば十分すぎる条件を意味します。

例えば、

• ジャニーズに所属しているための十分条件は？

と言われたら、「嵐のメンバーである」という事が分かれば十分過ぎるでしょうし、

• 18歳以上であるための十分条件は？

と言われたら「自動車の免許証を提示」できれば十分です。

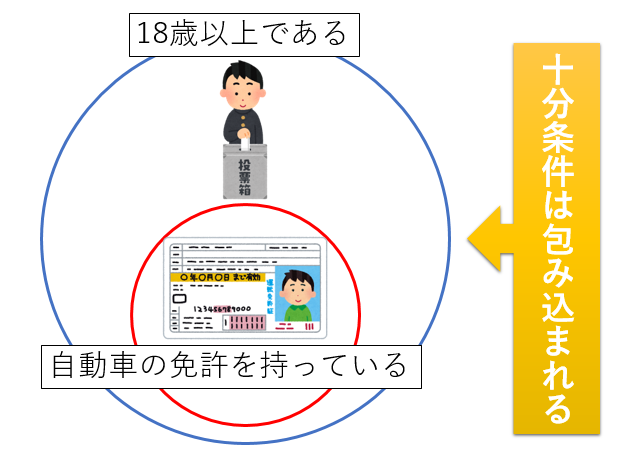
「18歳以上である」ための十分条件「自動車の免許を持っている」は、提示された条件「18歳以上である」にすっぽりと包み込まれている条件であるが重要なポイントです。

このように提示された条件よりもより厳しい条件のことを十分条件は意味しているというわけです。

これで必要条件と十分条件の意味が明らかになりました。

ここまでの内容が理解できたあなたは論理的な思考力が備わっていますので、ぜひ日常生活でも必要条件・十分条件の考え方を使ってみてください。

入試問題に挑戦！

それでは最後に必要十分条件に関する問題に挑戦してみたいと思います。 

x>0 は x>2 であるための何条件？

大学入試で必要十分条件を問われる際、「〇〇〇は、×××であるための何条件ですか」という形式で問われることがほとんどです。

必要条件なのか、十分条件なのか、はたまた必要十分条件なのかを判断するためには、問題で提示された２つの条件を図示できる場合は、図示します。

この問題の場合、与えられた条件「x>0」と「x>2」をそれぞれ数直線上に図示すると次のようになります。

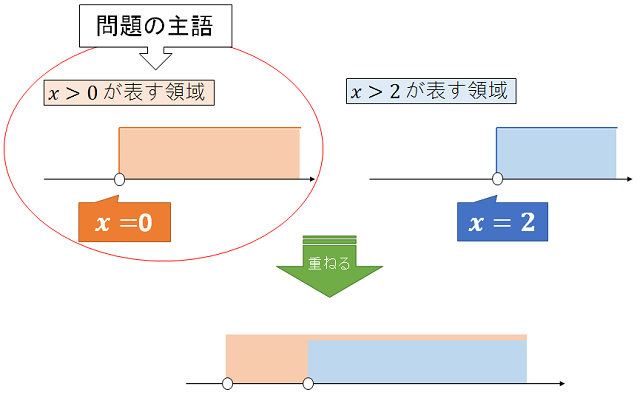
問題文を見ると、主語は赤丸で囲んだ「x>0」という条件ですので、こちらがもう一方の条件「x>2」を包み込んでいるのか、それとも包み込まれているのかを見破ればいいわけです。

この問題では主語の条件「x>0」がもう一方の条件「x>2」を包み込んでいることがわかるため、必要条件だが十分条件ではないという答えになります。

分かりましたか。それでは、もう一問挑戦してみましょう。

nが4の倍数は、nが偶数であるための何条件？

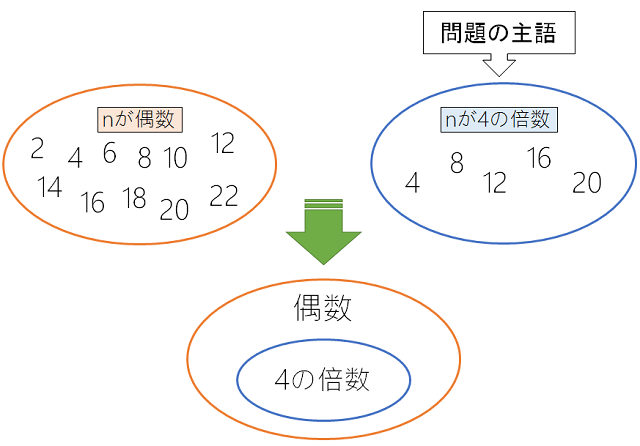
繰り返しになりますが、必要条件・十分条件を見破るためには、どちらがどちらを包み込んでいるのかが重要でした。

この問題では、主語の条件「nが4の倍数」であるがもうひとつの条件「nが偶数」に包み込まれていることが分かります。

以上より、必要条件ではないが十分条件であるという答えにたどり着くわけです。

必要十分条件のまとめ

「必要十分条件」について、その意味と覚え方について解説してきました。

まとめると

• 必要条件・十分条件の本質は２つの条件の構造把握
• 必要条件は、ある条件が成立するために必要な条件（包み込む）
• 十分条件は、ある条件を示すには十分な条件（包み込まれる）

ということになります。

提示された条件をクリアするために自分が取り組む案件が必要条件なのか、十分条件なのか把握することは次の一手につながるでしょうし、分析・調査結果を読み解く力にもつながります。

以上で、論理的思考力に欠かせない「必要十分条件の意味と覚え方」は終わりになります。

最後まで読んでいただき、ありがとうございました。