ドラえもんから学ぶ！指数関数の恐ろしさ

本日は、藤子・F・不二雄の漫画「ドラえもん*1」をネタに、指数関数と対数関数という高校数学の有用性を紹介できればと思います。

「ドラえもんと数学？」って不思議に思いますよね。

ですが、ドラえもんの17巻に登場する「バイバイン」という話は、数学的・物理的な現象として捉えると面白い考察できる内容になっているのです。

ということで、まずは今回取り上げる「バイバイン」という話について、簡単に紹介したいと思います。

バイバインの恐怖

ある日、のび太は１つの栗まんじゅうを前にして頭を抱えています。

「栗まんじゅうはおいしいんだけど、食べるとなくなっちゃうだろ。食べても無くならないようにできないかな…。」

またまた、のび太のわがままが始まりました。これに対して、優しいドラえもんは「バイバイン」という道具を出してあげます。

このバイバインという薬が凄いんです。バイバインを栗まんじゅうに振りかけると、食べない限り、5分で2倍に増やしてくれるのです。

その後、のび太君は欲を出し、栗まんじゅうを増やしてから食べようとします。

ところが、増えた栗まんじゅうでお腹一杯になったのび太は、ドラえもんに内緒でゴミ箱へ栗まんじゅうを捨ててしまうのです。

その後も増え続けていく栗まんじゅう。

増え続ける栗まんじゅうは、1時間でなんと4096個にも増えてしまいます。

それを見つけてビックリしたドラえもんは、宇宙の彼方へと栗まんじゅうを送ることで栗まんじゅうを処分するのです。

ここでバイバインのお話は終わっています。

バイバインの恐怖は続く

ドラえもんが栗まんじゅうを宇宙のかなたへ送って事なきを得た話となっているこの回の話ですが、現在の科学では宇宙は広がり続けてはいるものの有限な空間であることが知られています。

つまり、増え続ける栗まんじゅうでいつか宇宙は埋め尽くされてしまうのです。

果たして、それはいつでしょうか？

それでは、ここから数学的現象としてバイバインの話の続きを考察してみることにします。

宇宙のモデル化

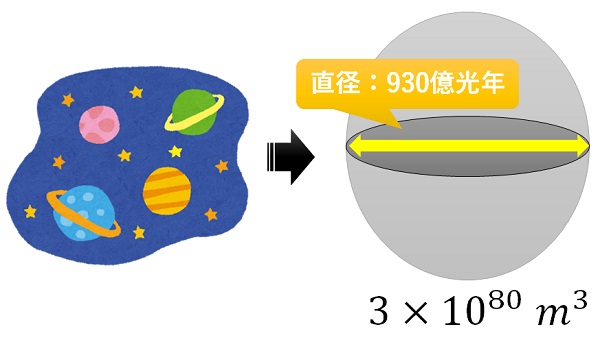
今現在、宇宙の大きさについては諸説あるようですが、宇宙が誕生してからは約137億年が経っており、その大きさは直径930億光年の球体*2と考えられていようです。

ここでは、この直径に対する球体の体積を宇宙の体積と定義したいと思います。

ちなみに、1光年とは光が1年間で進む距離で、光は1秒で地球を7周半しますから

• 1光年＝約9兆4600億km

にもなります。いかに宇宙が大きいか想像もできませんよね。

栗まんじゅうのモデル化

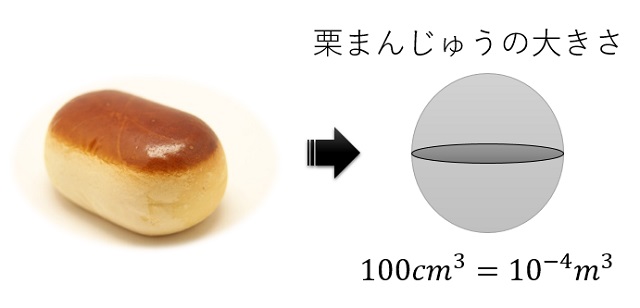
ここでは、栗まんじゅう1個の大きさを100㎤とすることにします。

この100㎤の栗まんじゅうが5分ごとに分裂して増えていくわけですから、その体積を数式化していきます。

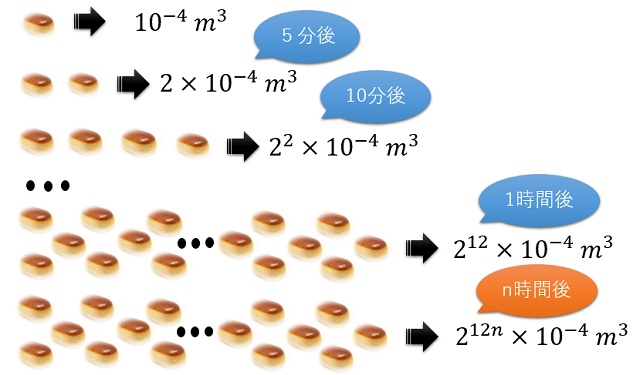
このように計算することで、n時間後の栗まんじゅうの体積を求めることができました。

バイバインで世界は滅ぶ

さて、本題に入っていきます。

増え続けていく栗まんじゅうの体積が宇宙の大きさと同じになるのは何時間後なのでしょうか。

この疑問を解くために、先ほど用意した「宇宙の体積」と「栗まんじゅうのｎ時間後の体積」を用いて等式を作ります。

それでは、この式を満たすｎを求めていきます。この計算過程で対数を用いていると、非常に計算が楽になります。

よって、n＝23.388時間となります。

つまり、ドラえもんが栗まんじゅうを宇宙の彼方へと飛ばしても、23時間30分後には宇宙中が栗まんじゅうによって埋め尽くされてしまうのです。

計算上では、ドラえもんの最終回は17巻ということになってしまいます。

こんな意見や解決策も…

一方で、現代宇宙理論や物理学的視点（ビッグバン理論や相対論、質量保存の法則など）に立つと、ここで紹介した数学的なモデルとは違った結論に到達します。興味がある方は、ぜひ調べてみてください。

他にも、ドラえもんの道具を駆使した解決方法も考えられます。

4次元ポケットに押し込んでもいいですよね。ドラえもん最強！

冗談はこのくらいにして、今回のバイバインの数学的考察から学んだことをまとめてみたいと思います。

数学的考察で伝えたいこと

ここで紹介したバイバインの話や計算過程を通じて、指数関数と対数関数の有用性が確認できました。

指数関数の有用性

まず、今回の考察の中で一番訴えたいことは「指数関数の発散速度」です。

5分で倍になる栗まんじゅうが、たった1個から宇宙を覆い尽くすまでに掛かる時間が23時間30分ということにビックリしませんでしたか。

これは指数関数の爆発的な増加を物語っています。

他にもこんな話が有名です。

指数関数に関する面白い話

新聞紙の話は、物理的に不可能ですが理論上こうなります。

米粒の話は曽呂利新左衛門という方が豊臣秀吉に褒美として提案した話になります。

数学的な話ですと

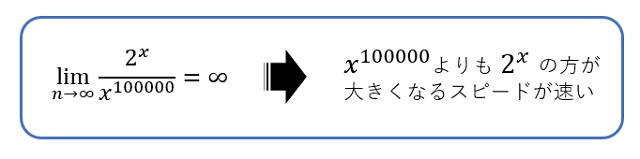
こんな式が成り立つことに指数関数の発散速度の速さを見ることができるかもしれません。

指数関数をグラフで書くと 

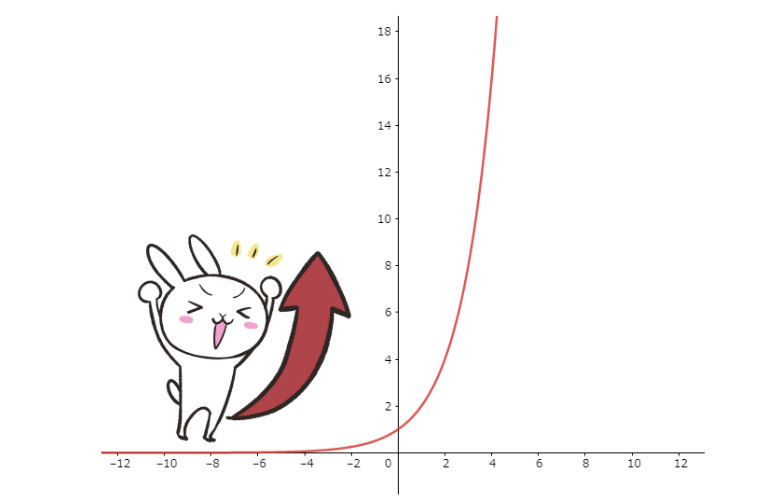
一気に大きくなっていく様子が見て取れます。

投資に興味がある方は、よく「複利投資は最強だ」という言葉を耳にするかと思いますが、複利も一種の指数関数です。そう考えると、複利が最強と言われる所以が分かりますよね。

対数関数の有用性

また、ここで紹介した計算過程の中で、威力を発揮した計算方法に「常用対数」が上げられます。常用対数とはlog（ログ）という記号です。

高校数学で学習する対数logを使うと、ここで行なった計算のように

• もの凄く大きい値
• もの凄く小さい値

を計算しやすい値に変換してくれるのです。

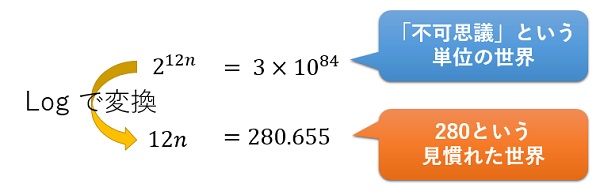
経済学や物理学等では非常に大きな値を対象にした計算が必須になります。そうしたときに、そのままの値で計算をしていくと、負荷が大きくなりすぎてしまうことがあります。

そんなときに対数logを使うことで、一気に扱う値を小さな値へと変換してくれるというわけです。これは計算上、非常に大きなメリットになります。

指数関数的に増えるは恐怖

ドラえもんという非現実的な世界を題材に、あくまでも数学的視点で「バイバインのその後」を考察してみました。

この考察で訴えたいことは、指数関数と対数関数の有用性だったわけですが、それぞれの特性をざっくりと理解するには良い教材だったかと思います。

現在も猛威をふるっている新型コロナウィルスや季節性のウィルスであるインフルエンザは時に指数関数的に感染者数を増やします。

指数関数はのび太が感じていたように、増え始めはゆっくりと上昇するため、安易に考え、行動してしまいがちです。

しかし、上昇に転じたときには想像を超える勢いで上昇していくことがバイバインの話からも感じられたのではないでしょうか。

指数関数的に変化する様々なものに対しては、早め早めに対策を講じることがいかに大切か。その考えをこの記事から学び、行動する方がいたら嬉しいです。

当ブログでは、数学の持つ魅力を数学好きな筆者なりにかみ砕いて発信しています。

2021年10月13日相関係数とは何か！求め方とその意味をドラえもんキャラを使って図解解説！

今後も数学に関する記事を発信できればと思っていますので、楽しみにしていてください。本日も最後まで読んでいただき、ありがとうございました。