相関係数(r)を求めるには、次の式を利用します。
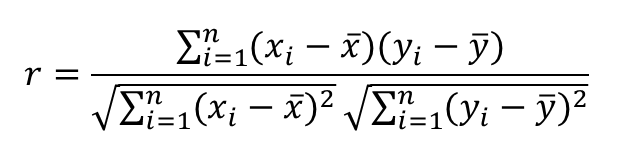
この式を使うことで、2つの(2次元)データ間にある関係性を数値化することができます。
といっても、この式で判定できる関係性は基本的に以下の3つのパターンです。
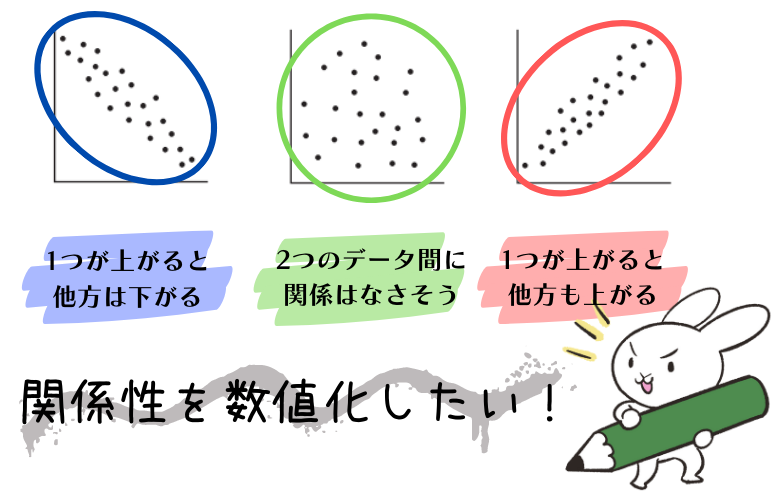
ここでは、この相関係数(r)を求める式をドラえもんに登場するキャラクターを使って図解しながら楽しく概念を理解できるように解説していこうと思います。
ここで学ぶ2つのデータ間の関係を読み解くことは、ビジネスや医療、投資など様々な分野において非常に高い価値があるテーマです。
そのため、統計学や数学が苦手なんだけど、相関係数くらいは知っておきたいというちょっと数字が苦手なんだけども・・・という方にも「相関係数とは何か」を理解してもらえることを目指しています。
相関係数を求める式の構造
相関係数の式は、一見とても複雑な形をしていますが、その構造は実にシンプルです。
ポイントはたった2つ。
分母の「標準偏差」の式と、分子の「共分散」の式です。
では、それぞれのポイントに目を向け、相関係数の式を読み解いていきましょう。
相関係数の分母は「標準偏差」
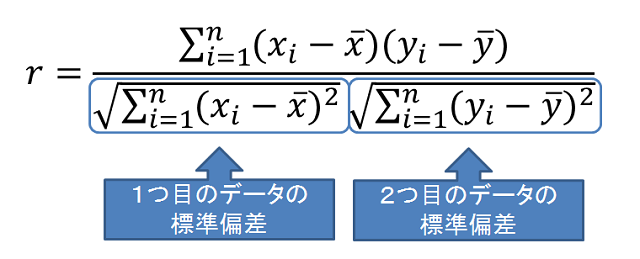
相関係数の式の構造で、まず押さえておくべきことは分母の式の持つ意味です。
この式は一見難しそうに見えますが、やっていることは標準偏差を求めるという作業を「x」というデータ群と、「y」というデータ群で各々行っているだけです。
標準偏差がそもそもよく分からないという方は、まずは「標準偏差とは何か」を理解することから始めることをおすすめします。
 標準偏差とは何か!その求め方と意味を図解で徹底解説
標準偏差とは何か!その求め方と意味を図解で徹底解説
相関係数の分子は「共分散」

次に、相関係数の式の分子に注目します。
相関係数の式の分子は、「共分散」と呼ばれる指標です。この共分散については後程詳しく説明します。
つまり、相関係数を求める式を理解するには、
- 標準偏差(分母)
- 共分散(分子)
という2つの指標さえ理解しておけばいいことになります。
相関係数の「相関」とは何か
相関係数を求める式の構造を解き明かす前に、相関係数とはどのような道具なのかについてもう少し明らかにしておきます。
相関の種類
相関とは2つのデータを対等に捉え、その2つのデータの間に
- 一方が増加すれば、それにしたがって他方も増加する
- 一方が増加すれば、それにしたがって他方は減少する
- 「気温」と「ビールの売上げ」
- 「学力」と「運動神経」
というように、2つのデータの間に相関関係があるのかどうかが気になる場面は多々あるわけです。
相関関係があると分かれば、対策を講じることができるわけですから重要な情報ですよね。
実際は、相関関係と因果関係は違うので注意が必要です。
相関を視覚的に把握する方法
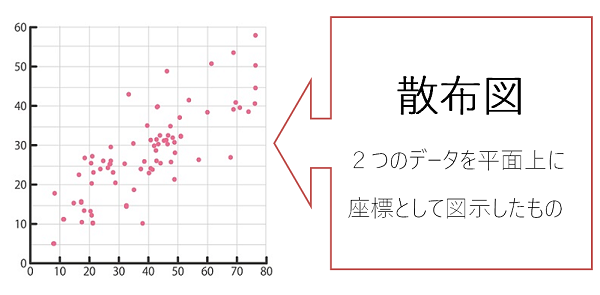
散布図を描く目的は、視覚的に相関関係を確認することにあります。散布図を描くことでパッと見て、2つのデータに相関関係があるかないかを大雑把に判断することができるわけです。
散布図を描くことで、パッと見の感覚的な捉えはできますが、似た図になったときに、どちらの相関の方が強いか判断に迷う場面があります。
こうした場面で、相関の強弱をしっかりと判断するためには、やはり相関関係を数値化する必要性があるわけです。
そこで、相関関係を数値化するために、「共分散」という指標にたどり着くわけです。
共分散とは何か
「共分散とは何か」の答えを先に言ってしまうと、共分散とは相関の有無を確認する指標です。
共分散を求めることで、2つのデータの間に、
- 一方が増加すれば、それにしたがって他方も増加する(正の相関)
- 一方が増加すれば、それにしたがって他方は減少する(負の相関)
- 関係性はない(相関がない)
のいずれの関係にあるかを数値化し、読み取ることができます。
では、どのようにして相関を数値化するのでしょうか。
共分散の意味
ここでは、「体力テスト」と「学力テスト」という2つのデータを例に挙げ、相関の数値化を目指してみることにします。
あるクラスで、「体力テスト」と「学力テスト」(いずれも100点満点)のテストを受け、その2つのデータを散布図にしたところ次のようになりました。
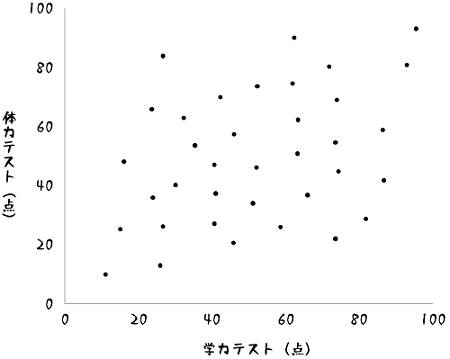
ここでこの散布図から「体力テスト」と「学力テスト」に相関がどれほどあるのかを数値化することが目標になります。
そして、相関を数値化するため、まずはそれぞれのデータ(体力テストと学力テスト)の平均点を求めます。
これは相関係数の式では、次の部分を求めていることになります。

それぞれのテストの平均点を求めたら、散布図内に平均点を線で書き込みます。
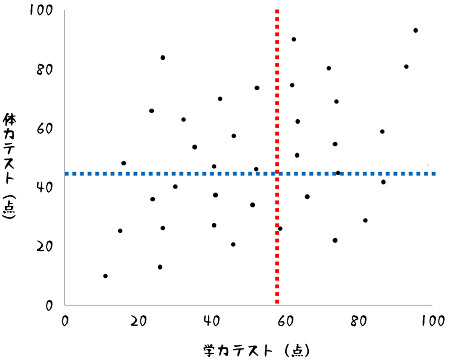
この平均点ラインを散布図に書き込むことで、散布図は4分割されました。
ここで、4分割された各ブロックの特徴をドラえもんのキャラクター達*1でイメージすると、次のようなイメージが持てます。
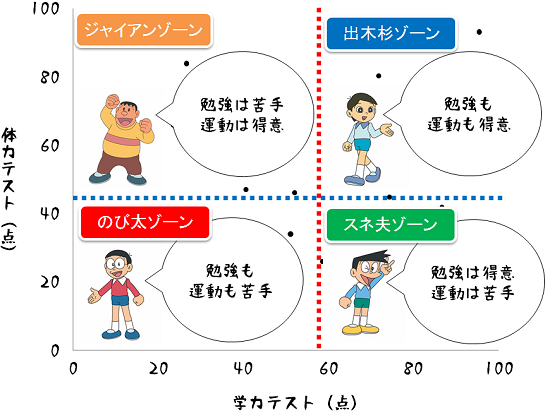
ドラえもんに登場するのび太、ジャイアン、スネ夫、出木杉のイメージで4分割された区間のイメージを共有できたところで、もう一度共分散の式を見つめてみることにします。
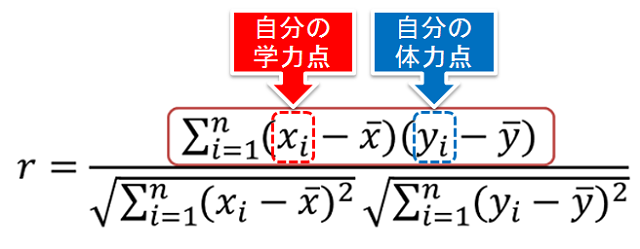
共分散の式をよく見ると、学力と体力のテストそれぞれで(自分の点数)ー(平均点)を計算し、掛け算していることが分かります。
そして、共分散では、この掛け算の答えの『符号(+・-)』に注目します。
4つのゾーンにおいて、掛け算の答えの符号をまとめたものが、次の表になります。
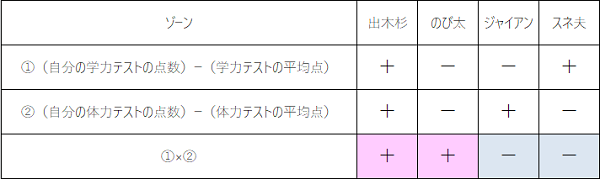
注目すべきは、
- 出木杉とのび太はプラス
- ジャイアンとスネ夫はマイナス
になっていることです。
正の相関が強いと共分散はどうなるのか
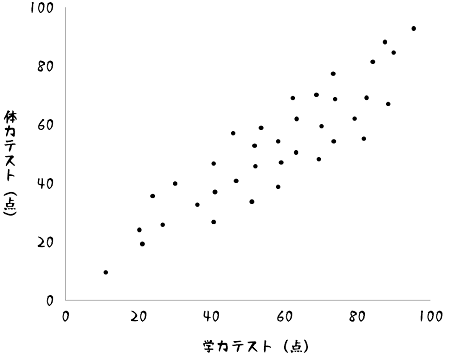
もしそれぞれのテストの散布図がこのようになった場合、共分散はどうなるのでしょうか。
この散布図を見ると、学力テストの点数が高いと体力テストの点数も高くなっていく正の相関があることが視覚的に確認できます。
これを先ほどの4分割とキャラクターで捉えるならば、このクラスには出木杉ゾーンの生徒ととのび太ゾーンの生徒が沢山いることになります。
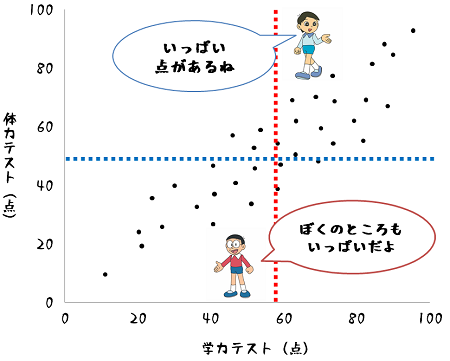
このような状態で、共分散を計算するとどうなるのでしょうか。

共分散の式を見てみると、Σ(シグマ)という記号があります。これは、足し算していくことを表した記号です。
先ほどの正の相関では出木杉ゾーンのび太ゾーンに入る生徒が多くいるのでした。

- 共分散「+」→正の相関
- 共分散「ー」→負の相関
- 共分散「0」→相関なし
このように、共分散の計算をすることで相関関係があるかないか判断できるというわけです。
ここで一つの疑問が浮かんできます。
「共分散で2つの関係性が読み解けるなら、相関係数なんていらないのでは・・・?」
確かにその通りです。
しかし、共分散には大きな欠点があるため、共分散を使おうとすると大きな問題が起こってしまいます。
この問題点について以下で説明します。
共分散の問題点
共分散を計算することで、相関関係のあるなしを把握することができることは分かったわけですが、共分散には次のような厄介な問題点が潜んでいます。
データの「単位」によって値が変化する
共分散の結果は、データの単位に依存してしまうことで、相関関係の「あるなし」は分かるのですが、「強弱」の判断ができないのです。
といわれてもピンと来ないので、共分散の復習も兼ね、あるクラス5人の「身長」と「体重」の共分散を計算してみることにします。
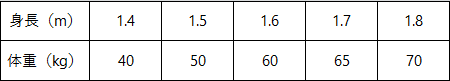
このクラスのデータをもとに、まずは身長と体重の平均値をそれぞれ求めます。
- 身長:(1.4+1.5+1.6+1.7+1.8)÷5=1.6(m)
- 体重:(40+50+60+65+70)÷5=57(kg)
この平均値から、4つのゾーンのどこに所属するのかを求めていきます。
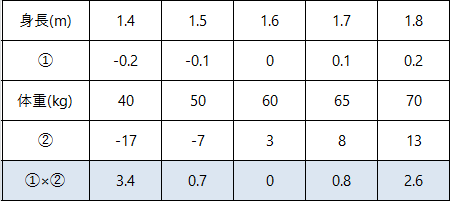
①:(自分の身長)-(身長の平均)
②:(自分の体重)-(体重の平均)
共分散は①×②の平均値ですので『1.5』となります。
次に、同じデータを
- 身長の単位:m→cm
- 体重の単位:kg→g
に変えて共分散を求めてみます。
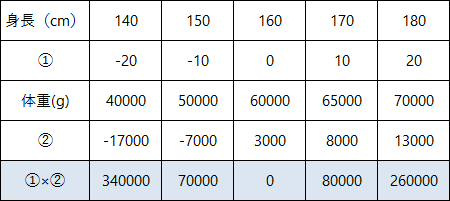
単位を変えた後の共分散①×②の平均値は『150000』となります。
このように、単位を変えたことで実質同じデータを取り扱っているにも関わらず、共分散の値が異なってしまうのです。
同じデータを扱っているのであれば、同じ相関なわけですから、これは非常に大きな問題です。
ということで、この問題点を解消するために共分散を加工した式こそが相関係数になります。
相関係数の式と意味
共分散の問題点を解消するために用いられる指標こそ、目標である「相関係数」になります。
相関係数とは、分子に共分散・分母に標準偏差という構造でした。

共分散は、扱うデータの単位に影響を受けてしまう指標だったため、共分散を単位の関係ない世界に引きずり込む必要があります。
単位に関係ない世界に引きずり込むことを、数学では『無名数化する』といいます。
つまり、共分散を無名数化するために、標準偏差で割っていることになります。共分散を無名数化し、相関係数を導き出したのはピアソンという数学者で、そのため相関係数は、ピアソンの積率相関係数という正式名が付いています。
相関係数の式を用いれば、先ほどの単位の違うデータ間の相関係数はどちらも『0.98』となり、一致することが確認できます。
共分散を無名数化した相関係数は、次のような規準で解釈されることが一般的(分野により異なる場合もある)です。
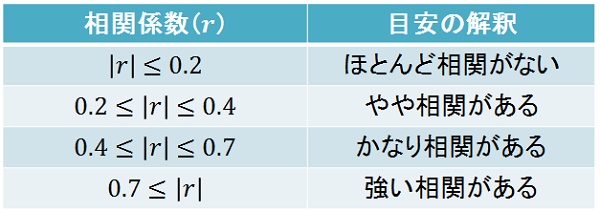
相関係数こそデータ分析の第一歩
ここでは、相関係数(r)について、その値を求める式をドラえもんに登場するキャラクターを使って図解しながら解説してきました。
かなり話が難しくなってしまったかも知れませんが、相関関係を知り、データ分析を行うことで様々な恩恵を享受することができます。実際、どんな恩恵が受けられるのかといった相関係数の実用性は以下の記事をご覧ください。
この記事をきっかけに、相関係数を色々なシーンで使ってみようと考えてくれる方がいたら嬉しいです。
*1:画像出典: ドラえもん|テレビ朝日


